
Variante del modelo
matemático de inventario de cantidad económica de pedido (CEP) considerando
estacionalidad de demanda
Variant of the mathematical economic
order quantity inventory model (CEP) considering seasonality demand
Gerald Antony Vicencio
Checco
Universidad Nacional Micaela
Bastidas de Apurímac, Perú
gvicencio@unamba.edu.pe
Dagnith Liz Bejarano Luján
Universidad Nacional Autónoma
de Tayacaja Daniel Hernández Morillo, Perú
lizbejarano@unat.edu.pe
Luis Ricardo Paredes
Quiroz
Universidad Nacional Micaela
Bastidas de Apurímac, Perú
lparedes@unamba.edu.pe
RESUMEN
La presente
investigación desarrolló un modelo matemático, variante del modelo de Cantidad
Económica de Pedido (CEP) en función de información histórica de demanda con
tendencia estacional. El objetivo fue calcular parámetros de tiempo y tamaño de
pedidos, de modo que estos pronósticos reduzcan costos y satisfagan la demanda
estimada sin conllevar gastos innecesarios. El modelo propuesto diseña pedidos
inicialmente en base al pronóstico de demanda futura a partir de información de
demanda histórica con tendencia estacional (suavizada, utilizando el método de
multiplicadores estacionales), posteriormente agrupa favorablemente los
periodos pronosticados (en función de los picos de demanda), establece
constantes logísticas y analiza los requerimientos en cada grupo recurriendo a
restricciones que permiten evaluar el volumen de pedidos de modo iterativo. Se
realizaron cuatro pruebas de análisis en diversos escenarios redefiniendo la
lógica de las restricciones. Los resultados presentaron un modelo matemático
que se desarrolló mediante procesos de iteración a partir de las restricciones
establecidas, concluyendo que con el modelo desarrollado es posible determinar
el volumen y los periodos óptimos para realizar estos pedidos en función de la
estacionalidad de la demanda. Siendo el modelo desarrollado una oportunidad de
investigación y desarrollo para la industria.
Palabras
clave: Demanda estacional, modelo de inventario,
cantidad económica de pedido, pronósticos de demanda.
ABSTRACT
This research
develops a mathematical model, a variant of the Economic Order Quantity (CEP)
model based on historical demand information for products with a seasonal
trend. The purpose is to calculate parameters of time and size of orders, so
that these forecasts reduce costs and satisfy the estimated demand without
entailing unnecessary expenses. The proposed model initially designs orders
based on the forecast of future demand based on historical demand information
with a seasonal trend (smoothed using the method of seasonal multipliers), then
the forecast periods are grouped favorably (based on demand peaks), establishes
logistical constants and analyzes the requirements in each group using
restrictions that allow the volume of orders to be evaluated iteratively; Four
analysis tests were carried out in different scenarios, redefining the logic of
the restrictions. The results presented a mathematical model that is developed
through iteration processes based on the established restrictions, concluding
that with the developed model it is possible to determine the volume and the
optimal periods to make these orders based on the seasonality of the demand.
Keywords: Seasonal demand; inventory
model; economic order quantity; demand forecasts.
INTRODUCCIÓN
En el contexto
actual de la industria, modelos de negocio priorizan la generación de valor y
tras observar el éxito logrado por sistemas de producción que trabajan de
manera colaborativa con sus proveedores y sus clientes como indica Darwish et
al. (2010), surgen conceptos como la gestión de cadena de suministros como
característica inherente a la actividad industrial, que busca integrar y
relacionar los procesos relativos a proveedores y comercializadores a fin de
cubrir demandas en torno a las necesidades del cliente final; en esta búsqueda
el planeamiento es una herramienta importante debido a que ayuda a programar
con anticipación requerimientos y planificar liberación de productos del stock
disponible.
Según Emigh
(1999) se ha desarrollado un creciente interés en implementar iniciativas de
inventarios administrados por el vendedor (vendor managed inventory, VMI), lo
que corrobora el interés de la industria en desarrollar procesos de manera
óptima que permitan reducir costos y planificar operaciones con anticipación,
para cubrir las demandas del mercado.
Diversos modelos
de inventario han sido estudiados (Causado, 2015; Rojas, 2013; Gutiérrez y
Vidal 2008), sin embargo, la variante del modelo matemático Cantidad Económica
de Pedido (CEP) considerando estacionalidad de demanda para productos ha sido
poco investigado.
La presente
investigación tiene como objetivo definir una variante del modelo de inventario
CEP para productos de demanda histórica estacional. Además, el modelo
desarrollado busca planificar pedidos anticipadamente, reduciendo el tiempo de
espera, de modo que permita mejorar los tiempos en los procesos, y facilitar la
coordinación y el control de inventarios.
METODOLOGÍA
Para el
desarrollo y validación del modelo matemático se siguió diferentes
procedimientos a fin de definir aspectos generales e indicadores de control que
intervienen en la modelación matemática, posteriormente se realizó un proceso
de validación con diversos escenarios para el modelo desarrollado, como se
describe:
1.
Pronosticar el comportamiento de la demanda a partir de información histórica
En vista que el
modelo planteado es aplicable a productos con demanda estacional, a partir de
información histórica referente a la demanda con tendencia estacional de un
producto, se realizó un pronóstico de demanda utilizando el método de
multiplicadores estacionales.
Según Chapman
(2006), un pronóstico de línea recta calculado utilizando un modelo de regresión
lineal no muestra la estacionalidad de la información; para incorporar la
estacionalidad en el pronóstico es necesario desarrollar multiplicadores
estacionales para cada trimestre. Siguiendo el procedimiento citado por
Chapman, primero fue encontrado la proporción de la demanda real respecto del
pronóstico de regresión, luego se calculó un promedio de estas proporciones
para los trimestres similares en periodos de análisis diferentes; y aplicando
los multiplicadores estacionales se obtuvo el pronóstico de regresión ajustado
estacionalmente. Sin embargo, fue observado en el estudio un margen de error
considerable al utilizar varios datos de información histórica en el pronóstico
de demanda por el método antes mencionado, por lo que primero se agrupó la
información histórica en grupos trabajando de esta manera con menos datos en
los grupos, reduciendo el error en el pronóstico.
La fiabilidad
del pronóstico de demanda está sujeto al tipo de producto debido a que otras
variables intervinientes (clima, ingreso del consumidor, inflación, etc.), no
consideradas en el estudio realizado deben de ser irrelevantes al consumo del
cliente.
2. Definir la
lógica de inventario más óptima en la gestión de cadena de suministros
Se definió la
estrategia más óptima que aseguraba un abastecimiento adecuado a un costo
mínimo, estableciendo así los tiempos de pedido más óptimos y los métodos de
distribución más apropiados.
3. Establecer
constantes logísticas y variables de control que faciliten el flujo de
productos por el almacén
Se relacionó la
lógica PEPS (lo que primero entra es lo que primero sale) en el modelo de
inventario que aseguraba la relevancia en el despacho de los lotes de pedidos
que ingresan primero. A partir de esta relación se establecieron variables de
control y constantes logísticas en nuestro modelo de inventario.
4.
Establecer la cantidad a mantener en función de la estacionalidad durante el
periodo de análisis
Se relacionó la
cantidad a mantener con la estacionalidad en términos sencillos durante el
periodo de análisis, para ello se recurrió a las constantes logísticas
establecidas anteriormente.
5. Definir la
relación del lote de pedido con el costo total en un modelo matemático con base
en el modelo CEP
Se estableció
una relación entre el tamaño del lote de pedido y el número de pedidos dentro
del periodo de análisis, considerando su implicancia en el costo total.
6. Optimizar
el modelo matemático a fin de determinar la cantidad optima de pedido y el
tiempo de pedido que minimicen el costo total
Con los
parámetros de tiempo y cantidad más óptima, se estableció una variante del
modelo matemático CEP considerando estacionalidad para una gestión optima de la
cadena de suministros.
7. Validar el
modelo de inventario
En función a las
condiciones descritas por Winston (1994), se realizó la validación de datos,
para lo cual se consideró el modelo optimizado descrito en series de tiempo más
extensas donde se demostró la repetitividad y continuidad en el modelo a
establecer. Las condiciones descritas por Winston (1994), para validar los
modelos de inventario indican que se debe satisfacer las siguientes hipótesis:
- Pedido repetitivo: La decisión de pedir se repite en forma regular.
Es decir, se coloca un pedido, y a medida que se consume el inventario se colocara
otro y así sucesivamente.
- Periodo continuo: Un pedido se puede hacer en cualquier ocasión. Los
modelos de inventario que permiten esto se llaman modelos de revisión continua.
Si la cantidad de inventario disponible se revisa en forma periódica y solo se
tienen pedidos en forma periódica, tenemos un modelo de revisión periódica.
Así mismo, este
modelo se aplicó en función a ciertas condiciones iniciales inherentes al
estudio:
- Debido a que el estudio realizado, consideró pronósticos de demanda
a partir de información histórica, utilizando para ello el suavizado de la
curva por medio de multiplicadores estacionales, resultó útil este estudio para
pronósticos en tramos cortos de tiempo, considerando para ello por lo menos 4
periodos trimestrales como máximo.
- La aplicación de este modelo de manejo de inventario, facilitó la
toma de decisiones, y el presente trabajo, recreó un escenario donde nos
permitió pronosticar los requerimientos y tiempos utilizados en nuestro
abastecimiento; en caso se aplique a un producto, la investigación tendría por
defecto un diseño experimental.
- Para que este modelo fuera aplicado en productos con estacionalidad,
el producto debería presentar picos de demanda presentes en la información
histórica, de similar forma en todo el periodo de análisis de la demanda
pronosticada, debería ajustarse a ciertas condiciones del modelo, pronosticando
requerimientos a los proveedores y facilitando la gestión de cadena de
suministro, ya que permitiría (a los proveedores) disponer de recursos en la
etapa de producción y abastecer de manera oportuna a la empresa, satisfaciendo
la demanda totalmente, evitando ventas perdidas, reduciendo los costos
inherentes a la actividad.
A partir de
estas condiciones iniciales y luego de desarrollar el modelo matemático, se
realizaron tres pruebas de validación en diferentes escenarios, y se analizaron
los comportamientos en función de las variables de control a fin de optimizar
parámetros del modelo desarrollado.
Modelo matemático basado en iteraciones a partir de un análisis de
bloques
A partir de datos históricos de la demanda (2 años de antigüedad)
con tendencia estacional para productos, se desarrolló un pronóstico de demanda
(S) suavizado estacionalmente para tramos delimitados por el punto de reorden
(generalmente cuando el stock disponible es cero), y posteriormente se analizó
en base a cuatro restricciones para determinar el volumen óptimo de pedido,
desarrollando así un análisis por bloques (Figura 1).
Figura 1
Análisis por bloque del modelo matemático de manejo de inventario
considerando estacionalidad de demanda

Nota: En la figura, N representa número de pedidos, S demanda total
pronosticada, r3 residuo optimizable, Qentrada volumen del pedido de entrada y
Qsalida volumen de pedido de salida.
En el bloque I (Figura 1) fue considerado un análisis de demanda en
función de la cantidad a pedir, por tanto, se optimizó el volumen de pedidos a
solicitar, asumiendo un análisis de 3 tramos delimitados por los puntos de
reorden (Figura 2).
Figura 2
Distribución en tramos de los bloques de demanda

Nota: En la
figura, para un determinado tramo, N representa número de pedidos, S demanda
total pronosticada, r3 residuo optimizable, Q volumen del pedido óptimo.
En el bloque II
(Figura 1) se analizaron cuatro restricciones, que permitieron que los valores
obtenidos sean reales y se ajusten al pronóstico de demanda existente.
El valor óptimo
de la primera restricción (Qsalida1) (Figura 3) se definió en función de
cualquier pedido ingresado (Qentrada), pronósticos de demanda (S1, S2, S3),
número de pedidos (N1, N2, N3) y restos de demanda no cubiertos en cada tramo
(r1, r2, r3), asegurando un inventario final igual a cero y un costo de
mantenimiento necesario.
Figura 3
Primera restricción con un volumen de pedido Qsalida 1

Nota: Donde,
S¬¬1: Demanda total pronosticada en el tramo I
S¬¬2: Demanda total pronosticada en el tramo II
S¬¬3: Demanda total pronosticada en el tramo III
N1: Número de pedidos en el tramo I
N2: Número de pedidos en el tramo II
N3: Número de pedidos en el tramo III
r1: Número de pedidos en el tramo I
r2: Número de pedidos en el tramo II
r3: Número de pedidos en el tramo III
El valor óptimo de la segunda restricción (Qsalida2) (Figura 4),
indicó que existía una condición optimizable dentro de cada tramo de análisis (g1; g2; g3), esta condición optimizable estuvo
en función de cada uno de los restos (r1, r2, r3) y en base al valor del
volumen óptimo (Q).
De este modo se
definió 3 volúmenes óptimos de pedido con el resto optimizado (Qoptimo I,
Qoptimo II, Qoptimo III); y se definió el valor máximo de estos volúmenes
óptimos, como aquel que satisface la demanda en todos los periodos.
Figura 4
Segunda
restricción con un volumen de pedido Qsalida 2

Donde:
Q optimo I: Volumen de pedido con resto optimizado en
el tramo I
Q optimo II: Volumen de pedido con resto optimizado en
el tramo II
Q optimo III: Volumen de pedido con resto optimizado
en el tramo III
γ I: condición optimizable en el tramo I
γ II: condición optimizable en el tramo I
γ III: condición optimizable en el tramo I
Para la tercera restricción, el valor optimo (Qsalida3) (Figura 5),
satisface la demanda pronosticada en el primer periodo del primer tramo (R1),
de modo que, desde un inicio, cumpla con los requerimientos. De esta manera los
excedentes del pedido se pueden dosificar para los periodos siguientes.
Figura 5
Tercera
restricción con un volumen de pedido Qsalida 3
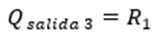
Nota: Donde,
R1: pronóstico
de demanda suavizado estacionalmente para el periodo “1”
La cuarta
restricción (Figura 6) tuvo como factor limitante el número de periodos dentro
de cada tramo de análisis, por ello se restringió la demanda total pronosticada
en su totalidad para cada tramo, en función del número máximo de pedidos que se
puede realizar en cada tramo.
Figura 6
Cuarta
restricción con un volumen de pedido Qsalida 4
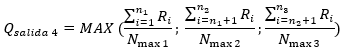
Nmax I: Número máximo de pedidos en el tramo I
Nmax II: Número máximo de pedidos en el tramo II
Nmax III: Número máximo de pedidos en el tramo III
NI: Número de periodos en el tramo I
NII: Número de periodos en el tramo II
NIII: Número de
periodos en el tramo III
Finalmente, se definió el volumen optimo (Qsalida) (Figura 7)
como el valor máximo de los valores apropiados, encontrados en los análisis de
las cuatro restricciones antes descritas. De este modo se tuvo:
Figura 7
Volumen de pedido
óptimo Qsalida 2
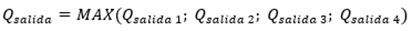
Nota: Donde,
Qsalida: Volumen de pedido de entrada
MAX: Mayor valor
de los valores obtenidos en las restricciones.
DISCUSIÓN
En el desarrollo del presente modelo matemático a partir de
pronósticos de demanda con tendencia estacional, se ha establecido una serie de
condiciones que permiten su implementación, estas condiciones son recurrentes
en el desarrollo de las variantes del modelo de Cantidad Económica de Pedido
(CEP) lo que concuerda con Yao et al. (2007) que indican que los modelos
desarrollados complementan y extienden trabajos previos que surgen de la teoría
clásica de Cantidad Económica de Pedido. Para reducir costos en el modelo
desarrollado se realizó un análisis de restricciones definidas a partir de la
dinámica del inventario y luego se recurrió a las iteraciones para calcular el
valor optimo mediante el comportamiento de las variables utilizadas, este
procedimiento estuvo fundamentado en las investigaciones realizadas por Liu et
al. (2004) que buscaron resolver los problemas de optimización con
restricciones no-lineales que capturan puntos clave de la dinámica de los
sistemas complejos de producción e inventarios, desarrollando un modelo de
múltiples etapas de colas en los inventarios y el sistema de producción, con el
objetivo de minimizar los costos de inventarios a lo largo de la cadena.
Para evaluar la optimización de la cantidad a mantener se estableció
un indicador de control denominado Factor de Optimización (FOP), pues el manejo
de inventario intenta optimizar la cantidad a mantener, por lo tanto, este
indicador mide unidades almacenadas como parte del stock disponible, entonces
enfocando nuestros esfuerzos en reducir los productos a mantener en nuestro
almacén podemos reducir los costos de mantener y por ende reducir los costos
totales. Resultados similares, aplicado al área de producción, fueron obtenidos
por Kapuscinski et al. (2004) que diseñaron un sistema de gestión para la toma
de decisiones de los inventarios de la cadena de suministro de la empresa Dell
Computers, que no manejaba inventarios de producto terminado, concluyendo que
debería enfocar sus esfuerzos al control de los componentes.El modelo
desarrollado es de revisión continua pues permite realizar pedidos en cualquier
ocasión, además por la naturaleza de la lógica de inventario establecido por
tramos en la distribución de pedidos en todos los periodos de análisis, se
puede indicar que en el tramo de análisis se busca cubrir toda la demanda
existente, por lo que en periodos iniciales del tramo siguiente el pedido será
de tipo obligatorio, este comportamiento es repetitivo en todos los tramos de
análisis, concordando con las condiciones establecidas por Winston (1994).
CONCLUSIONES
Es posible definir una variante del modelo de Cantidad Económica de
Pedido (CEP) considerando estacionalidad de demanda, que permita determinar el
volumen óptimo de pedido de productos a proveedores, satisfaciendo la demanda
pronosticada y minimizando los costos, a través de un análisis de dos bloques en
serie y análisis de cuatro restricciones. Estas restricciones estuvieron
basadas en función del comportamiento de la estacionalidad de la demanda, por
lo que al generarse un proceso iterativo en el uso de este método es posible
encontrar una convergencia en un valor optimo que minimiza los costos y que
pronostica los tiempos de reabastecimiento óptimos para realizar los pedidos;
mediante el análisis de la lógica de manejo de inventario y definiendo los
tramos presentes en el pronóstico de demanda. Siendo el modelo desarrollado una
oportunidad de investigación y desarrollo para la industria.
REFERENCIAS
BIBLIOGRÁFICAS
[1]
Causado, E.R. (2015). Modelo de inventarios para
control económico de pedidos en empresa comercializadora de alimentos. Revista
Ingenierías Universidad de Medellin, 14(27), 163-178.
[2]
Chapman, S. N. (2006). Planificación y control
de la producción. Editorial Pearson Educación de México. ISBN: 970-26-0771-X.
[3]
Darwish, M. & Odah, O. (2010). Vendor
managed inventory model for single-vendor multi-retailer supply chains.
European Journal of Operational Research 204(3), 473-484.
[4]
Emigh, J. (1999). Vendor-managed inventory:
Financial and business concepts in brief. Computerworld, 33/34(21), 52-55.
[5]
Gutiérrez, V., Vidal, C.J. (2008). Modelos de
Gestión de Inventarios en Cadenas de Abastecimiento: Revisión de la Literatura.
Rev. Fac. Ing. Uni. Antioquia, 43, 134-149.
[6]
Kapuscinski, R., Zhang, R. Q., Carbonneau, P.,
Moore, R., & Reeves, B. (2004). Inventory decisions in Dell's Supply Chain.
Interfaces, 34, 191-205.
[7]
Liu, L., Xiaoming, L., & Yao, D. (2004).
Analysis and Optimization of a Multistage Inventory-Queue System. Management
Science, 50(3), 365-380.
[8]
Rojas, D. A. Aplicación de la Teoría de
Inventarios a una empresa Poblana. (Tesis de pregrado, Benemérita Universidad
Autónoma de Puebla.
https://www.fcfm.buap.mx/assets/docs/docencia/tesis/ma/AreliRojasDeGante.pdf.
[9]
Winston, W. (1994). Investigación de
operaciones, aplicaciones y algoritmos. Grupo Editorial Iberoamerica. México
D.F.
[10] Yao, Y., Evers, P. & Dresner, M. (2007). Supply chain
integration in vendor-managed inventory. Decision Support Systems 43(2),
663-674.




